Dans ce second article de la série, nous allons explorer quelques cas d’application des bases apprises dans le premier article. On va voir comment les utiliser pour analyser la ligne de départ, comment faire des choix lors des bascules de vents…

Mais tout d’abord, afin de pouvoir quantifier nos gains et ou nos pertes, examinons comment avec notre principe des échelles comment mathématiquement ce qui se passe sur l’eau peut se traduire.

Principe du levier

Nous savons, quand le vent est stable, classer les bateaux tirant des bords vers la bouée grâce au principe de la perpendiculaire. Dans la suite, nous tentons de répondre à la même question, lorsque le vent varie. Lorsqu’il y a deux bateaux, il est généralement admis que, dans une situation de refus, le bateau situé sous le vent et en avant prend l’avantage. Pour visualiser cela, imaginez vos mains tendues devant vous, puis inclinez vos poignets vers la gauche. Vos mains représentent le bord tribord et votre main gauche vient de prendre de l’avance. Un autre exemple pour poser le problème : pour le vent réel 1, les bateaux B et C sont à égalité. Si le vent réel passe en 2 (rotation à gauche, adonnante pour B, refusante pour C) et y reste, que se passe-t-il ? On notera que la bascule est telle que les deux bateaux continuent à tirer des bords vers la marque, aucun d’eux n’est hors du cadre pour la nouvelle direction du vent. 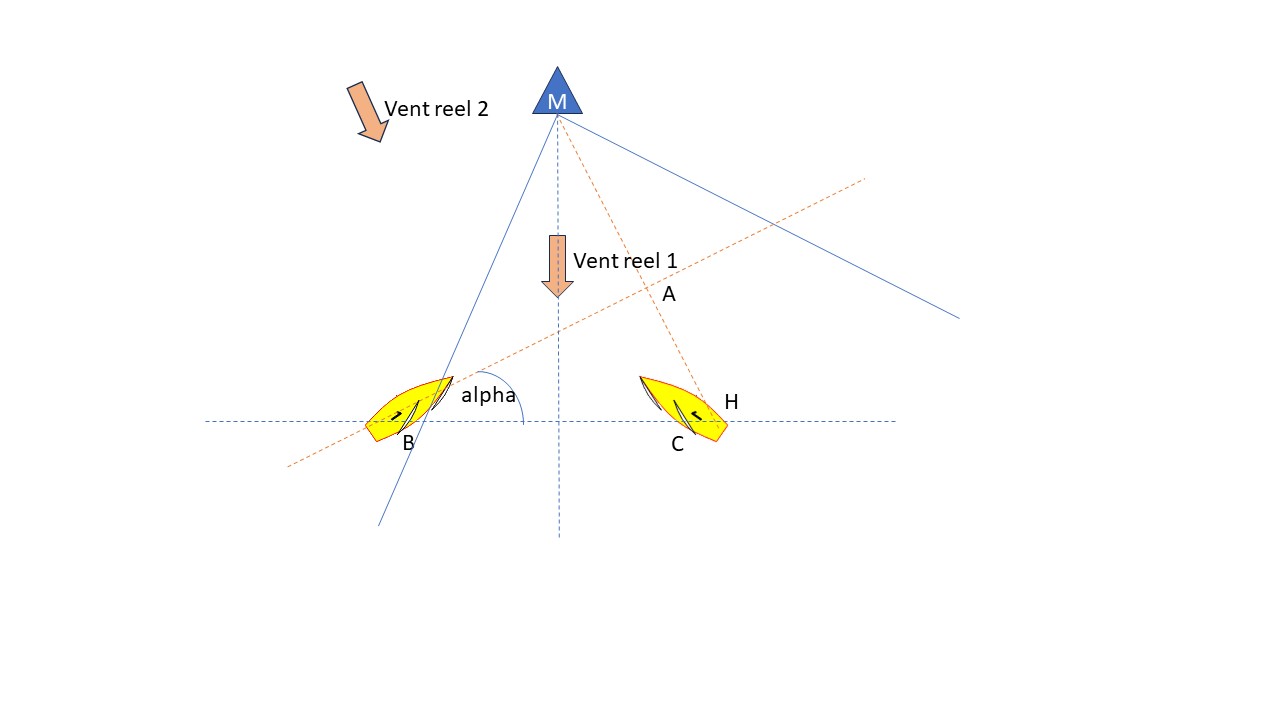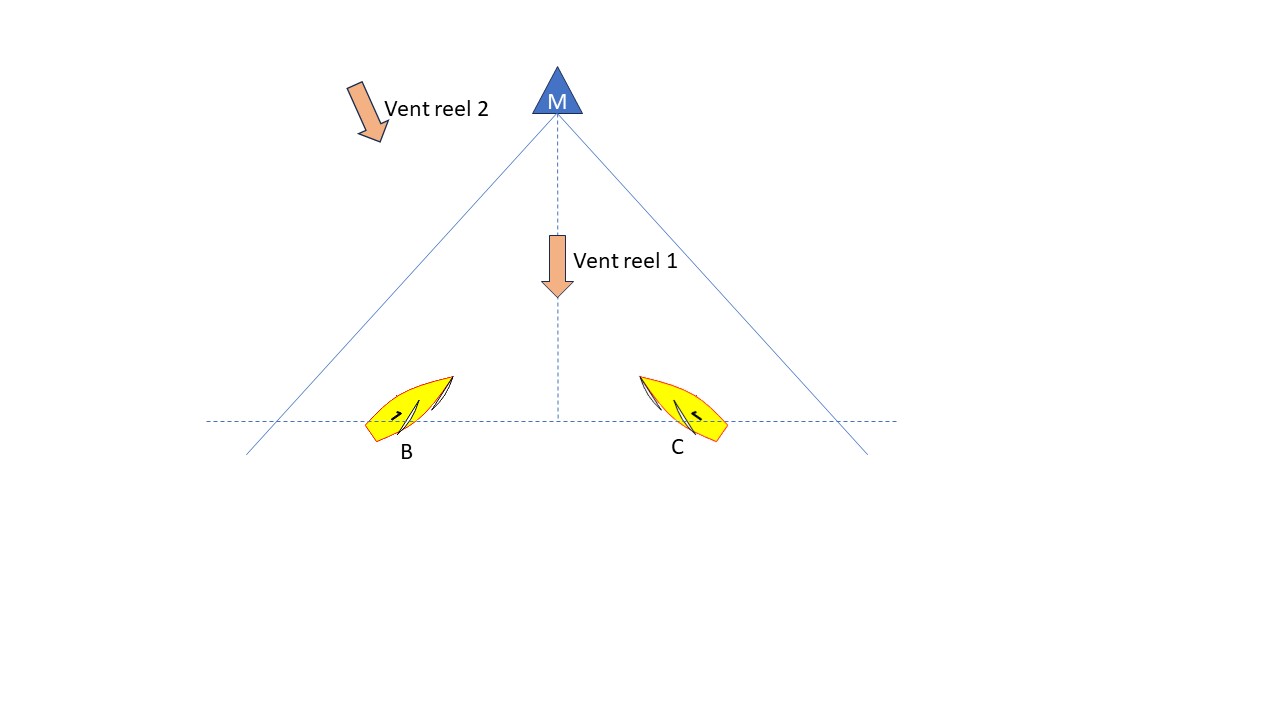Levier et bascule La réponse est simple : appliquons le principe de la perpendiculaire à la nouvelle situation : on voit tout de suite que B sera devant C, et nous pouvons même calculer l’écart (AH, il vaut BH * sin(alpha), si alpha est l’angle de la bascule). Calcule math

Ordre de grandeur des gains

Au prés, pour un bateau ayant 90° d’angle mort et pour une bascule de 20°, le gain procuré par une tactique judicieuse sur la tactique catastrophique est de l’ordre de 20 %, c’est-à-dire 1 mille sur un parcours d’une heure au prés pour un bateau de régate moyen !

Le tableau suivant montre les gains.

On voit bien que le gain croît très vite avec l’angle de la bascule. De quelques pour cent pour des angles faibles, il peut atteindre la moitié de l’écart pour un angle de 30°. Par exemple un écart de 500 m en latéral se transforme pour une bascule de 20°, en une avance de 170 m si vous êtes du bon côté.

Notez que l’on a supposé que les deux bateaux continuent de tirer des bords vers la marque après la bascule. Les conclusions seraient différentes si l’un des bateaux pouvait faire route directe.

Applications du principe du levier

Le levier au prés et tactique

Examinons quelques situations typiques :

dans le cas où les 2 bateaux sont à égalité, en cas de refus (rotation gauche), le bateau Jaune va gagner la distance en fonction du tableau, dans le cas d'une adonnante (rotation à droite) c'est le bateau Bleu qui gagne.

si le bateau sont alignés l'un dernière l'autre, c'est le bateau Jaune qui gagne en refus et le Bleu dans l'adonnante

S'ils sont directement sous le vent l'un de l'autre : le Bleu gagne dans les 2 cas, autant en adonnante qu'en refus.

Enfin, s'il y en a un qui est sous le vent de l'autre, le Jaune gagne dans les adonnantes, et le Bleu dans les refus.

On peut résumer ces règles de la façon suivante :

En tirant des bords au prés sur la même amure, il faut se placer du côté des adversaires d’où on espère le vent. Si on attend une adonnante, se placer à leur vent et si on attend un refus se placer sous leur vent.

B attend un refus. Il crée de l’écart et se place sous le vent de C

E attend une adonnante. Il crée de l’écart et se place au vent de D

C’est le principe du levier et il s’énonce ainsi :

Si deux bateaux tirent des bords au près, lors d’une rotation de vent, le bateau qui est du côté du nouveau vent est gagnant. Il est d’autant plus gagnant que la bascule est importante et que l’écart latéral entre les deux bateaux est important. Ce dernier joue comme un levier.

Petit rappel :

Adonnante : Un vent qui tourne dans une direction favorable, permettant au bateau de se rapprocher de son cap sans changer de bord.
Refusante : Un vent qui tourne dans une direction défavorable, obligeant le bateau à s’éloigner de son cap ou à changer de bord.

Le levier au portant

Le problème se pose de la même façon, du moins en théorie. Les différences principales proviennent de la faiblesse de l’angle mort.

Si deux bateaux tirent des bords au portant, lors d'une rotation de vent, le bateau qui est du côté opposé au nouveau vent est gagnant. Il est d'autant plus gagnant que la bascule est importante et que l'écart latéral entre les deux bateaux est important. Ce dernier joue comme un levier. Là encore, on suppose que les bateaux continuent à tirer des bords de grand largue vers la marque après la bascule.

pour le nouveau vent 2, A est devant B de la distance BH

Le principe du levier est légèrement différent au portant. Au lieu de favoriser le bateau situé du côté de la bascule, il favorise le bateau situé du côté opposé à la bascule.

Il s’énonce ainsi :

Au portant :

Il faut tirer à l’inverse du près, c’est-à- dire s’éloigner du nouveau vent en premier.

À cause de la faiblesse de l’angle, on devra aussi se méfier de ne pas être dans le cas d’exception pour l’application.

La ligne de départ

Quand la ligne de départ n’est pas perpendiculaire au vent, plus elle est grande, plus le gain obtenu en partant du bon côté est important.

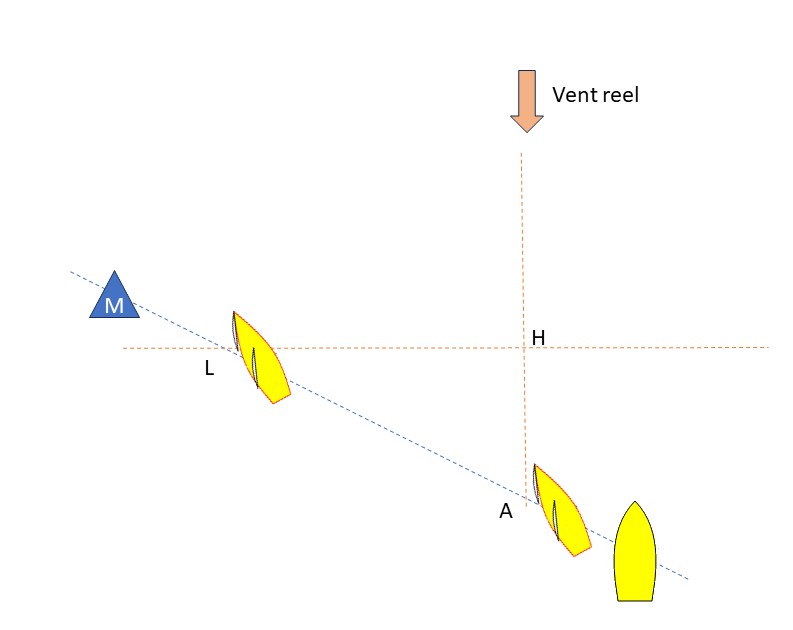
Avantage ligne

Le bateau L du bon côté de la ligne a d’emblée l’avance AH sur son poursuivant, Une ligne longue de 50 m, biaisée de 10°, procure un avantage de 8.5 m, soit une longueur de bateau pour beaucoup.

Remerciement à Jean-Yves Bernot

Les bases : cas d'utilisations pratiques